LICZBA KOMÓREK W PLASTRZE PSZCZELIM I SPOSOBY JEJ OBLICZENIA

Kilka lat temu, gdy zacząłem bliżej interesować się rozwojem rodziny pszczelej, znalazłem się w dość kłopotliwej sytuacji. W literaturze prawie powszechnie twierdzono, że matka pszczela znosi od 1500 do 2000 jajeczek dziennie. Natomiast jeśli chodzi o liczbę komórek w plastrze pszczelim, to podawano, że w 1 cm2 mieszczą się przeciętnie 4 komórki pszczele, w 25 cm2 około 100 komórek pszczelich.

W innych źródłach natomiast, że w plastrze wielkopolskim mieści się 6850 komórek, w 1 cm2 plastra mieszczą się 4 komórki pszczele lub 3 komórki trutowe, a w 1 dcm2 mieści się 400 komórek. Porównując ze sobą te wielkości, nabrałem podejrzeń co do ich prawdziwości. Już na pierwszy rzut oka widać, że twierdzenie jakoby w 1 cm2 mieściły się 4 komórki, jest fałszywie. Zatem, jak na przykład można było obliczyć nieśność matki pszczelej, jeżeli nie potrafiło się dokładnie obliczyć ile komórek mieści się w jednym plastrze pszczelim? Dlatego postanowiłem to zagadnienie dokładnie przeanalizować, dokonać obliczeń, a wyniki opisać, aby już więcej nie było pod tym względem żadnych wątpliwości.

Teoria

W ulach ramowych, a obecnie tylko takie są w powszechnym użytkowaniu, produkcja plastrów pszczelich oparta jest wyłącznie na wykorzystywaniu węzy jako podstawowej bazy do dalszej budowy komórek pszczelich przez pszczoły woszczarki. Dlatego naukowe wywody stwierdzające, że wymiary komórek pszczelich są zmienne i zależą od rasy pszczół, nie mają w tym przypadku żadnego znaczenia. Pszczoły budują komórki o wymiarach takich, jakie są wytłoczone na arkuszach węzy.

W produkowanych obecnie arkuszach komórka ma wymiar 5,5 mm (odległość równoległych boków sześcioboku). Liczbę komórek w plastrze po obu jego stronach można obliczyć dwoma sposobami.

polega na obliczeniu podwójnej powierzchni plastra i podzieleniu jej przez obliczoną powierzchnię komórki.

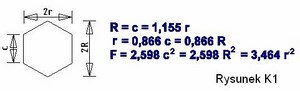
R - związane jest z okręgiem opisującym sześciokąt.
r - związane jest z okręgiem wpisanym w sześciokąt.
h - wysokość trójkąta równobocznego w sześciokącie (5,5/2=2,75)
Obliczamy powierzchnia komórki:

znając c=3,17 otrzymamy powierzchnia komórki p=26,20mm2
W przypadku ramki wielkopolskiej, mającej wymiary wewnętrzne 340 x 240 mm, obustronna powierzchnia plastra P = 340 x 240 x 2 = 163200 mm2, a liczba komórek wyniesie
P/p = 163200/26,2 = 6229.

polega na obliczeniu, ile komórek mieści się na szerokości i długości plastra.
Pomnożenie tych liczb przez siebie da liczbę komórek na jednej stronie plastra. Podwojenie tej liczby określa liczbę komórek w całym plastrze.

Problem tylko w tym, że jeżeli jeden bok plastra podzielimy przez szerokość komórki, to drugiego boku już nie możemy dzielić przez szerokość komórki, lecz przez wartość
t = ~4,76. Zatem jeżeli jeden bok dzielimy przez 5,5 to drugi przez 4,76.

W tym przypadku otrzymamy następujący wynik:
340 / 5,5 = 61,818
240 / 4,76 = 50,420
61,818 x 50,42 x 2 = 6233
Różnica pomiędzy wynikami z pierwszego i drugiego sposobu obliczenia wynika z zaokrągleń ułamkowych. 6233 – 6229 = 4 komórki.

Gdy w uproszczeniu zamiast 61,818 i 50,420 przyjmiemy 62 i 50, to otrzymamy 62 x 50 x 2 = 6200 sztuk komórek.

Poprawność podanych powyżej sposobów obliczania, jest wystarczająco uzasadniona przedstawionymi na rysunkach wzorami matematycznymi

2F / f = 2F / 26,20

[...] - część treści ukryta, w całości dostępna tylko dla zalogowanych e-Prenumeratorów

Czesław Suchcicki

Zamów prenumeratę czasopisma "Pasieka"